Statistiek achtergrond
Voordat we met Schadeverzekeringen beginnen, gaan we eerst in de onderstaande paragrafen een opfriscursus doen van wiskunde en statistiek. Deze studiestof heb je nodig om het beroepsproduct makkelijk te kunnen uitvoeren.
Voor dit gedeelte wordt gebruik gemaakt van de inhoud van het boek ‘Introductory statistics with applications in general insurance‘ van (I.B. Hossack; J.H. Pollard en B. Zehnwirth).
1) Wiskunde basisvaardigheden
- Sommatie betreft het optellen van een grpoep cijfers of getallen. Hiervoor kun je de volgende website benaderen: Sommatie.
- Faculteit n! is het product van de eerste n positieve getallen. Hiervoor kun je de volgende website benaderen: Faculteit.
- Binomiaalgetallen komen voor in het binomium van Newton en dat verklaart de naam hiervan. Hiervoor kun je de volgende website benaderen: Binomiaalgetallen. Vooral de volgende algemene formule is belangrijk voor integer, niet-integer, positieve of negatieve x.
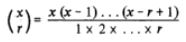
- Machten. Hiervoor kun je de volgende website benaderen: Machten.
- Afgeleiden. Hiervoor kun je de volgende website benaderen: Afgeleiden.
- Maximum en minimum van functies met één of meedere variabelen berekenen. Max. en Min. door afgeliede.
- Exponentiële functies. Hiervoor kun je de volgende website benaderen: Exponentiële functies.
- Naturaal logaritmische functie LN(x). Hiervoor kun je de volgende website benaderen: Logaritmische functies.
2) Variabele schalen
Om een passende statistische methode te kunnen vinden voor een bepaalde variabele, dienen we eerst de variabele schaal te weten. Er zijn vier type schalen:
- Nominale schaal (kleur van een auto; merk van een schoen)
- Ordinale schaal (antwoordmogelijkheden van een vraag, 1=goed ; 2=matig en 3=slecht)
- Intervalschaal (temperatuur of tijd van klok)
- Ratioschaal (wachttijd in de wachtkamer; gewicht per persoon)
Dit betreft de statistiekkennis van hoofdstuk 1.1 van het boek ‘Statistiek om mee te werken‘ (Arie Buijs).
3) Ligging en Spreiding
Dit betreft de statistiekkennis van hoofdstuk 2 van het boek ‘Statistiek om mee te werken‘ (Arie Buijs).
Voor een extra toelichting kun je op het volgende linkjes klikken:
- Toelichting ‘Centrum- en spreidingmaten I’
- Toelichting ‘Centrum- en spreidingsmaten II’
- Toelichting ‘Centrum- en spreidingsmaten III’
3.1 Verwachtingswaarde van discreet en continu stochast.
Dit betreft de statistiekkennis van hoofdstuk 4.3.1 en 4.6 van het boek ‘Statistiek om mee te werken‘ (Arie Buijs).
Zie hiervoor ook de voorbeelden tijdens de lessen van Schadeverzekeringen.
De verwachtingswaarde wordt aangeduidt met E(X) of μ(X):
E(X) = x1 · P(X = x1) + x2 · P(X = x2) + … xn · P(X = xn)
3.2 Variantie van discreet en continu stochast.
Dit betreft de statistiekkennis van hoofdstuk 4.3.2 en 4.6 van het boek ‘Statistiek om mee te werken‘ (Arie Buijs).
Zie hiervoor ook de voorbeelden tijdens de lessen van Schadeverzekeringen.
De variantie van stochast X is de verwachtingswaarde van de kwadraten van [xi – E(X)]. De standaardafwijking is de wortel van de variantie.
3.3 Momenten van discreet en continu stochast.
Zie hiervoor ook de voorbeelden tijdens de lessen van Schadeverzekeringen.
- Algemene formule voor momenten: Y = 1/n * Σ(X-mu)^k
- Tweede centrale moment van een verzameling: Y = 1/n * Σ(X-mu)^2
- Derde centrale moment: Y = 1/n * Σ(X-mu)^3
Voor extra theoriestof en toelichting zie onderstaande linkjes:
3.4 Scheefheid
Het begrip scheefheid (Engels: skewness) is in de statistiek de meestgebruikte maat van asymmetrie. Scheefheid is zowel te berekenen voor een kansverdeling als een steekproef.
4) Elementaire kansen
Dit betreft de statistiekkennis van hoofdstuk 3 (vooral paragraaf 3.1 en 3.2) van het boek ‘Statistiek om mee te werken‘ (Arie Buijs).
- Volgordeproblemen
- Permutaties
- Variaties
- Combinaties
- Groepen na teruglegging
- Inleiding kansrekening
- Kansdefinities: Filmpje ‘Kans definitie’ of Filmpje ‘Wat is kansrekening?’
- Rekenregels voor kansen
- Voorwaardelijke kansen: Filmpje ‘Voorwaardelijke kansen’ of Voorwaardelijke kansen
5) Stochasten
Een toevalsvariabele is een variabele waar bij elke waarde een bepaalde kans hoort dat die waarde optreedt. In plaats van toevalsvariabele zeg je ook wel stochast. Zie hiervoor: Stochast of toevalvariabele.
Dit betreft de statistiek kennis van hoofdstuk 4 (vooral paragrafen 4.1, 4.2 en 4.6) van het boek ‘Statistiek om mee te werken‘ (Arie Buijs).
Voor een extra toelichting kun je op het volgende linkje klikken: Filmpje toelichting stochast
5.1 Discrete stochast
Een discrete stochast is een stochast die een eindig aantal mogelijke waarden kan aannemen. Zie hiervoor: Discrete kansmodellen.
5.2 Continu stochast
Een toevalsvariabele X die alle reële waarden uit een bepaald interval [a,b] kan aannemen noem je een continue stochast. Zie hiervoor: Continue kansmodellen.
Voor een extra toelichting op discrete & continue toevalvariabelen kun je op het volgende linkje klikken: Filmpje toelichting ‘Discrete en continue kansvariabelen’
6) Voorwaardelijke Verwachting en Variantie
In de kansrekening geeft de voorwaardelijke verwachting of conditionele verwachting van een stochastische variabele, gegeven een gebeurtenis, aan wat de verwachting van de variabele zal zijn, als we ons beperken tot de gegeven gebeurtenis (bron: Wikipedia).
- Filmpje ‘Conditional expectattion toelichting’
- Filmpje ‘Conditional expectattion voorbeeld’
- Toelichting voorwaardelijke verwachting I
- Toelichting voorwaardelijke verwachting II
- Toelichting voorwaardelijke verwachting III
7) Verdelingen
Hieronder wordt een toelichting gegeven op het meeste gebruikte verdelingen bij schadeverzekeringen (druk hieronder op ‘Lees meer’):
- Normale verdeling
- Lognormale verdeling
- Gamma verdeling
- Poisson verdeling
- Pareto verdeling
7.1 Normale verdeling
Dit betreft de statistiekkennis van hoofdstuk 5 van het boek ‘Statistiek om mee te werken‘ (Arie Buijs).
Voor een extra toelichting op de Normale-verdeling kun je op de volgende linkjes klikken:
- Toelichting op Normale-verdeling
- Toelichting Centrale limietstelling
- Standaardiseren van Normale-verdeling
- Z-scores opzoeken in Normale-verdeling tabel
Zie hiervoor ook de voorbeelden tijdens de lessen van Schadeverzekeringen.
Voorbeeld 1: Een stochast X is Normaal-verdeeld met gemiddelde 3,6 en standaarddeviatie 1,2. Wat is de kans dat X tussen 4,2 en 5,6 ligt?
Voorbeeld 2: Een stochast X is Normaal-verdeeld met gemiddelde 3,6 en standaarddeviatie 1,2. Wat is de kans dat X tussen 1,2 en 5,4 ligt?
7.2 Lognormale verdeling
De Lognormale verdeling is een continue kansverdeling met de volgende belangrijke eigenschappen:
- Positieve scheefheid naar recht.
- Stochast X heeft een Lognormale verdeling met gemiddelde μ en standaarddeviatie σ, als Y = LN(X) Normaal verdeeld is met gemiddelde μ en standaarddeviatie σ.
- Domein X is (0, +∞), domein van Y is (-∞,+∞)
Deze kansverdeling wordt bij schadeverzekringen vaak gebruikt voor het modelleren van de schadehoogte.
Voor een extra toelichting op de Lognormale-verdeling kun je op de volgende linkjes klikken:
- Toelichting Lognormale verdeling I
- Toelichting Log-normale verdeling II
- Toelichting Log-normale verdeling III
7.3 Poisson verdeling
Dit betreft de statistiekkennis van hoofdstuk 7 van het boek ‘Statistiek om mee te werken‘ (Arie Buijs).
Voor een extra toelichting op de Normale-verdeling kun je op de volgende linkjes klikken:
Zie hiervoor ook de voorbeelden tijdens de lessen van Schadeverzekeringen.
7.4 Gamma verdeling
Zie hiervoor ook de voorbeelden tijdens de lessen van Schadeverzekeringen.
7.5 Pareto verdeling
Zie hiervoor ook de voorbeelden tijdens de lessen van Schadeverzekeringen.
Voor een extra toelichting kun je op het volgende linkjes klikken:
- Toelichting Pareto principe
- Toelichting Pareto verdeling (NL I)
- Toelichting Pareto verdeling (NL II)
- Toelichting Pareto verdeling (Engels)
- Voorbeeld opgave Pareto-verdeling
10) Steekproeven
Een steekproef of monster, een statistisch begrip, is een selectie uit een totale populatie ten behoeve van een meting van bepaalde eigenschappen van die populatie. In het dagelijkse spraakgebruik kan een monster ook een voorbeeld van één individu uit een populatie betekenen (bron: Wikipedia). Zie verder:
11) Betrouwbaarheidsintervallen
Betrouwbaarheid is in statistische toepassingen de mate waarin een meting vrij is van meetfouten (bron: Wikipedia). Zie verder:
12) Toetsen van Hypothesen
Vaak worden uitspraken over de hele bevolking gedaan op basis van een steekproef. Dat brengt natuurlijk risico’s met zich mee. Immers ook als (bijvoorbeeld) in werkelijkheid 15% van de bevolking het afgelopen jaar griep heeft gehad, kan in een steekproef door toevallige omstandigheden dit percentage wel eens anders liggen. Hoe kun je zo een steekproef gebruiken om te schatten hoeveel grieppatiënten er zijn geweest? (bron: math4allview).
