Risk management
Risk management praktijk
- Basel III: Europese wetgeving met als doel om de financiële gezondheid van banken te waarborgen.
- Solvency II: Is het nieuwe, risicogebaseerde toezichtraamwerk voor verzekeraars dat per 1 januari 2016 in werking is getreden. Een belangrijk doel van de Solvency II is het beschermen van de polishouders.
Value at risk(V@R)
Wat is de V@R definitie?
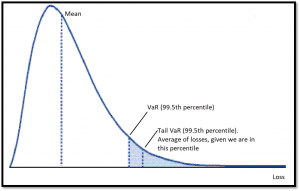
Het maximale verlies dat kan ontstaan op een positie door normale marktbewegingen in een bepaalde periode, gebaseerd op een ‘time to close’ benadering, uitgaande van een vastgesteld betrouwbaarheidsinterval [Jorion, 2001].
Time to close: de periode die nodig is om de portefeuille te liquideren. De kleinste periode bedraagt één dag.
Het maximale verlies dat kan ontstaan op een positie door normale marktbewegingen in een bepaalde periode, gebaseerd op een ‘time to close’ benadering, uitgaande van een vastgesteld betrouwbaarheidsinterval [Jorion, 2001].
Hoe wordt de V@R berekend?
- Parametrische methode:
- In het verleden vaak gebruikt.
- Alleen voor normale verdeling voldoet, normale verdeling het risico op extremen onderschat.
- Historische simulaties:
- Wordt vooral bij banken gebruikt.
- Zijn geen aannames nodig voor verdeling of correlaties.
- Complexe berekeningen (tijdrovend).
- Weinig datapunten.
- Monte-Carlosimulaties
- Meeste gebruikte methode nu.
- Goede aannames m.b.t. correlaties (copula’s) en keuze marginale verdeling.
Parametrische benadering V@R
V@R parametrische benadering (Z & BI)
- Er wordt verondersteld dat het risico normale verdeling heeft.
- We berekenen de Z-waarde bij een bepaalde betrouwbaarheidsniveau maal σ of gemiddelde.
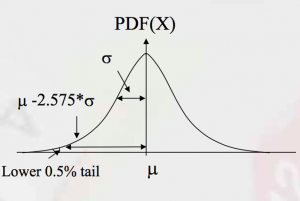
- De normale verdeling onderschat het risico op extremen.
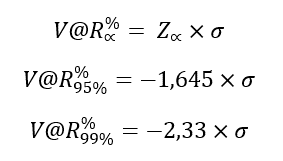
V@R parametrische benadering (Z, BI & €)
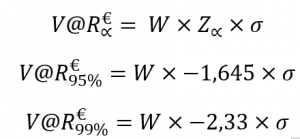
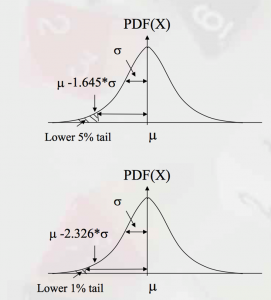
V@R parametrische benadering (Z, BI, € & n)
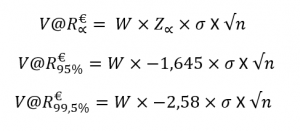
CV@R definitie
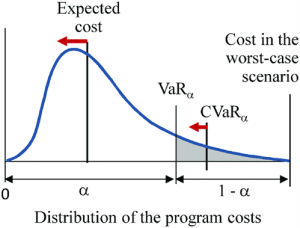
Conditional Value at Risk (CV@R), Ook wel het verwachte verlies genoemd, is een risicobeoordelingsmaatregel die de hoeveelheid staartrisico van een beleggingsportefeuille kwantificeert.
CV@R wordt afgeleid door een gewogen gemiddelde te nemen van de “extreme” verliezen in de staart van de verdeling van mogelijke rendementen, voorbij V@R.
CV@R benadering
We berekenen de CV@R voor een normale verdeling met een eenvoudige methode op de waarde van Z:
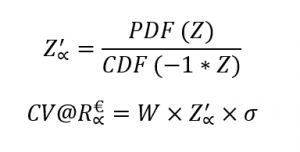
Historische benadering V@R
- Wordt vooral bij banken gebruikt.
- Geen aannames zijn nodig voor verdeling of correlaties.
- Complexe berekeningen (tijdrovend).
- Weinig datapunten.
Aan de hand van een voorbeeld gaan we deze methode bekijken.
De historische benadering doen we aan de hand van een voorbeeld voor één portefeuille. Voor twee en meer wordt de berekening moeilijker…
- Ga naar ELO en open het oefenbestand in de map les 4.
- Sla de gegevens op als een Excel-bestand.
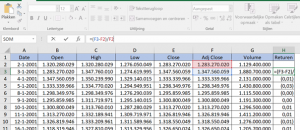
- Herleid de return van de rendementen per dag van de kolom ‘ Close’. R_(t+1)=((R_(t+1)-R_t))/R_t
- Teken de grafiek van de return. Wat valt je op?
- Kopieer kolom Return naar een nieuwe blad.
- Sorteer de return in het nieuwe blad van klein naar groot.
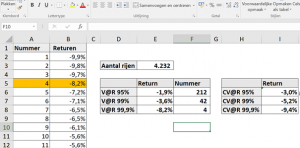
- Herleid de V@R voor 1%, 5% en 10% met een inleg van €1 mln.?
- Herleid CV@R voor 1%, 5% en 10% met een inleg van €1 mln.?
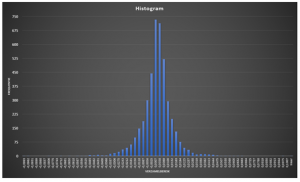
- Maak een histogram van de return. Wat valt je op?
Monte-Carlosimulatie V@R
De Monte-Carlosimulatie is een simulatietechniek waarbij een fysiek proces niet één keer maar vele malen wordt gesimuleerd, elke keer met andere startcondities (Wikipedia).
Dus de simulatie met verschillende beginaannames heel vaak herhalen (bijvoorbeeld 100.000 keer). Als 85% van de uitkomsten dezelfde resultaten geeft, dan weet je dat de gevonden uitkomst het meeste waarschijnlijk is.
Monte-Carlosimulaties worden ook bij het voorspellen van weersverwachting gebruikt.
Eenvoudig voorbeeld Monte-Carlosimulatie
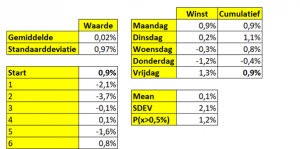
- Bereken het gemiddelde en de standaarddeviatie.
- Verwacht rendement per dag: =NORM.INV.N(ASELECT();GEM;STDEV)
- Verwacht rendement per week: cumulatief over 5-werkdagen.
- 5000 trekkingen met terugleggen: Gegevenstabel via Wat-als analyse.
- Gemiddelde en standaarddeviatie van 5000 simulaties. En P(x>0,5%).
Solvency Kapitaal vereiste (SCR)
Solvency II
Solvency II is het nieuwe, risicogebaseerde toezichtraamwerk voor verzekeraars dat per 1 januari 2016 in werking is getreden.
Doel
Een belangrijk doel van de Solvency II is het beschermen van de polishouders.
Raamwerk
- Pilaar 1 richt zich op de kwantificeerbare risico’s en bijbehorende voorzieningen en kapitaaleisen.
- Pilaar 2 focust zich op het risicomanagement en de bedrijfsvoering van een verzekeraar.
- Pilaar 3 omvat de eisen ten aanzien van te publiceren informatie en de rapportage aan de toezichthouder.
Richtlijnen
- Level 1: Solvency II-richtlijn inclusief amendementen.
- Level 2: Uitvoeringsverordening Solvency II.
- Level 2,5: Technische Standaarden.
- Level 3: EIOPA Richtsnoeren.
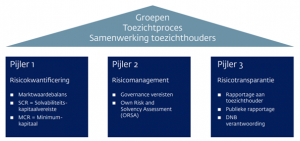
Solvency II pilaar 1
Pilaar 1 richt zich op de kwantificeerbare risico’s en bijbehorende voorzieningen en kapitaaleisen.
- Marktwaarde balans.
- SCR en MCR berekeningen.
Richtlijnen
- Level 1: Solvency II-richtlijn inclusief amendementen.
- Level 2: Uitvoeringsverordening Solvency II.
- Level 2,5: Technische Standaarden.
- Level 3: EIOPA Richtsnoeren.
SCR-definitie
Solvency Capital Requirement (SCR) is in essentie niets anders dan een V@R met een betrouwbaarheidsniveau van 99,5% en een aanhoudingsperiode van een jaar.
Solvency II risico’s
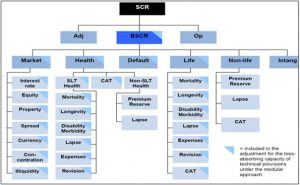
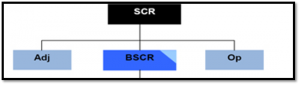
BSCR (Basis SCR)
-
- Kapitaalseis voor Marktrisico (Markt).
- Kapitaalseis voor Zorgrisico (Health).
- Kapitaalseis voor Tegenpartij creditrisico (Default).
- Kapitaalseis voor Levensverzekering technische risico’s (Life).
- Kapitaalseis voor Schadeverzekering technische risico’s (Non-Life).
- Kapitaalseis voor immateriële activa risico’s (Intangible).
Operationeel risico
Betreft het risico dat ontstaat als gevolg van het falen of tekortschieten van interne processen, menselijke en technische tekortkomingen, en onverwachte externe gebeurtenissen.
Adjustment (aanpassing voor belasting en winstdeling)
