1.1.1 Random Component: de Exponentiële Familie

Bij een GLM behoort de afhankelijke variabele bij een kansverdeling. Aangenomen wordt dat deze kansverdeling behoort tot de exponentiële Familie.

De exponentiële familie is een klasse kansverdelingen. De normale, exponentiële, gamma- en Poisson-verdeling behoren onder anderen allemaal tot deze klasse.

De willekeurigheid van een antwoord wordt als volgt weergeven:

y_i ~ Exponentieel( µ_i ,ɸ)

Het woord Exponentieel is een plaatsvervanger voor de daadwerkelijke kansverdeling waar y_i toe behoort. Hierna volgen twee parameters.

De µ staat symbool voor het gemiddelde van de verdeling. Deze representeert de verwachte uitkomst. De schatting van deze parameter is het uiteindelijke resultaat wat uit een GLM komt.

Als er niks anders bekend is van de records dan de uitkomst, dan is de beste schatter voor µ het gemiddelde van resultaten in het verleden. Ondanks dit kun je bij een GLM met behulp van predictor variabelen een betere schatting uitrekenen die uniek is voor elk risico. Dit is gebaseerd op de statistische relatie tussen de predictors en de target variables van historische data. Als je nog eens kijkt naar de formule voor y_i dan is te zien dat er een i staat bij de µ. Dit houdt in dat de µ record-specifiek is. De andere parameter, ɸ, anderzijds wordt van aangenomen dat deze hetzelfde is bij elke record.

1.1.2 Het Systematisch Component

Een GLM modelleert de relatie tussen µ_i (de verwachting van het model) en de predictors (x_i) al volgt:

g(µ_i) = β₀ + β₁x_i1 + β₂x_i2 + … + β_px_ip

De verhouding stelt dat de transformatie van een µ_i gelijk is aan de intercept (β₀) gesommeerd met een lineaire combinatie van predictors (x_i ; i = 1 t/m p) en coëfficiënten (β_i ; i = 1 t/m p). Deze coëfficiënten worden geschat door een GLM-programma.

De transformatie van µ_i, weergegeven door de functie g(.) aan de linkerkant van de verhouding, wordt de link function genoemd. Deze link function wordt bepaald door de gebruiker.

De rechterkant van de verhouding wordt de linear predictor genoemd. Wanneer deze uitgerekend is brengt hij de waarde op voor g(µ_i).

De link function biedt flexibiliteit aan voor het relateren van de verwachting aan de predictors. Bij een GLM is een getransformeerde waarde van µ_i gelijk aan de predictors. Ondanks dit moet de verwachting wel gelijk zijn aan de lineaire combinatie van de predictors. Hier komt het ‘lineaire’ gedeelte van een GLM vandaan.

Door een flexibiliteit toe te voegen aan deze verhouding worden meer opties vrijgesteld voor het model. Hierdoor wordt er een mogelijkheid gegeven om een verdeling te vinden die het best past bij de realiteit van de data.

Wanneer een GLM gebruikt wordt voor het opzetten van een verzekeringsplan wordt de link function een natuurlijk logaritme: g(x) = ln(x). Dit wordt een log link genoemd. De verhouding ziet er dan als volgt uit:

ln µ_i = β₀ + β₁x_i1 + β₂x_i2 + … + β_px_ip

Om nu µ_i uit te rekenen moet van deze verhouding de inverse genomen worden. Dit ziet er als volgt uit:

µ_i = e ^{(β0 + β1xi1 + β2xi2 + … + βpxip)}            ó          µ_i = e ^β0 * e ^β1xi1 * e ^β2xi2 * … * e ^βpxip

Nu is er een regel waarin de predictors met elkaar worden vermenigvuldigd (een multiplicatieve functie). Multiplicatieve modellen zijn het meest gebruikelijk voor deze zogenoemde rating structures.

1.3.1 Standard Error

De standard error is een geschatte standaarddeviatie van het proces. Een lage standaarddeviatie geeft aan dat de geschatte coëfficiënt dicht bij de daadwerkelijke waarde ligt en geeft dus aan dat de schatting realistisch is. Precies andersom is ook te zeggen dat een hoge standaarddeviatie zegt dat de geschatte coëfficiënt waarschijnlijk niet dicht bij de daadwerkelijke waarde ligt. Dit kan volbracht zijn door de willekeurigheid van de waarden.

1.3.2 p-waarde

De p-waarde is een significantietoets die een kans weergeeft. Deze kans reflecteert de mogelijkheid op de geschatte waarde (of hoger) wanneer de daadwerkelijke coëfficiënt gelijk is aan nul. Wanneer deze p-waarde laag is geeft dit dus aan dat de kans op het krijgen van de verkregen schatting laag is. Te concluderen is dus dat de waarde van de schatting waarschijnlijk niet het resultaat is van complete willekeurigheid en dus een realistisch beeld geeft van de daadwerkelijke waarde voor de coëfficiënt.

Er wordt getoetst op een nulhypothese die luidt: H₀: x = 0.

In principe wordt dus getoetst of de getoetste predictor invloed heeft op de verkregen data. De variabele is dan significant. Meestal wordt aangenomen dat wanneer de p-waarde lager is dan 0,05 dat de predictor daadwerkelijk een effect uit oefent op de data.

1.3.3 Betrouwbaarheidsinterval

De nulhypothese hoeft niet per sé te toetsen of de coëfficiënt gelijk is aan nul. De nulhypothese kan toetsen of de coëfficiënt gelijk is aan elk te bedenken getal. Hierbij komt het betrouwbaarheidsinterval te pas. Bij een drempelwaarde van 0,05 als p-waarde komt een 95%-betrouwbaarheidsinterval te pas. Alle waarden voor de coëfficiënt die binnen dit interval liggen zullen niet worden afgekeurd. Het bereik van dit interval wordt gezien als een redelijk bereik voor de schatters.

1.4.1 Werken met continue variabelen

Werken met een continue variabele is erg simpel. Elke continue variabele wordt zoals hij gegeven wordt in de GLM gestopt. Hier komt vervolgens per variabele één coëfficiënt uit. Hierdoor krijgt de linear predictor een lineair verband met de waarde van de predictor.

Bij een log link is het vaak gewoonlijk om de continue variabelen te loggen (‘logging continuous variables’). Dit houdt in dat de natuurlijke logaritmes van de continue predictors in het model worden gebruikt in plaats van de originele waarde. Dit ziet er als volgt uit:

ln µ_i = β₀ + β₁ ln x_i1 + β₂ ln x_i2 + … + β_p ln x_ip

Om µ_i af te kunnen leiden ziet de linear predictor er als volgt uit:

µ = e^β0 * e^{β1 ln xi1} * e^{β2 ln xi2} * … * e^{βp ln xip}

wordt

µ = e^β0 * x_i1^β1 * x_i2^β2 * … * x_ip^βp

1.4.2 Werken met categoriale variabelen

In de linear predictor wordt hiervoor gebruik gemaakt van binaire predictors: wanneer je te maken hebt met een bepaalde categorie zal voor deze bijbehorende coëfficiënt een 1 staan. Voor alle andere categorieën staat voor de coëfficiënt een 0.

Hierbij komt nog wel de situatie van pas dat alle predictors hiervan 0 zijn. Dit is het geval voor de base level; een categorie die van tevoren is gekozen. De coëfficiënten van de andere categorieën zijn gerelateerd aan de base level. Hierbij is de coëfficiënt van de base level als het ware ‘1’. Om de beste relaties aan te kunnen tonen is het belangrijk om als base level een categorie te kiezen met veel of de meeste records.

1.7.1 Verdelingen voor de hoogte van de claims of gebeurtenissen

Twee verdelingen die meestal worden gebruikt bij het bepalen van de hoogte van de claims/gebeurtenissen zijn de ‘Gamma’ verdeling en de ‘Inverse Gaussian’ verdeling.

Gamma verdeling

De gamma verdeling wordt gekenmerkt door een rechts scheve verdeling. Dit betekent dat het grootste deel van de populatie links van het gemiddelde ligt. Dit is terug te zien in de grafiek. De verdeling heeft ook een daadwerkelijk nulpunt. Het gemiddelde wordt gekenmerkt met het teken µ. De variantie functie bij deze verdeling is V(µ)= µ^2. In grafiek A1 ziet u hoe de grafiek zich gedraagt bij aanpassingen van de variantie.

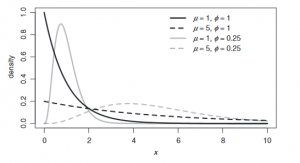
Grafiek A1: De gamma verdeling

Inverse Gaussian verdeling

De Inverse Gaussian verdeling komt erg overeen met de Gamma verdeling, alleen heeft deze verdeling een scherpere piek en een andere variantie functie; namelijk V(µ)= µ^3. De Inverse Gaussian verdeling heeft net als de Gamma verdeling een nulpunt. In grafiek A2 is te zien hoe de grafiek varieert als de spreiding groter en kleiner wordt eveneens als de variantie functie groter of kleiner wordt. Ook is de verhouding met de Gamma verdeling te zien in grafiek A2.

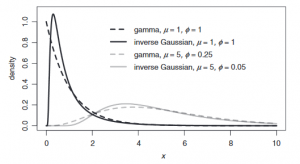
Grafiek A2: Inverse Gaussian verdeling

1.7.2 Verdelingen voor Frequentie

De bekendste verdeling voor het berekenen van de frequentie van een claim is de Poisson verdeling, maar er is ook een minder bekende: de Negatief Binomiale verdeling.

Poisson verdeling

Omdat een GLM fractionele waardes toelaat kan de Poisson verdeling, die discreet verdeeld is, toch gebruikt worden. Bij een model waar de frequentie van de claims van bepaald moeten worden is dit erg handig.

De variantie functie van de Poisson verdeling is: V(µ)= µ. Aangezien de variantie hetzelfde is als het gemiddelde betekent dit dat de spreiding altijd 1 zou moeten zijn. De variantieformule is dus bij de Poisson verdeling gelijk aan: Var[y]= µ.

Ondanks dit zit er toch een groot nadeel aan de Poisson verdeling. Er kan namelijk sprake zijn van overspreiding. Dit houdt in dat de variantie groter is dan het gemiddelde. Dit kan voorkomen wanneer er twee varianties gebruikt worden. Om hier alsnog mee te kunnen rekenen kan er gekozen worden te werken met een ODP (‘overdispersion Poisson’) -verdeling. Deze verdeling is in principe hetzelfde als de Poisson verdeling, alleen mag de spreiding elk positief getal aannemen.

Negatief Binomiale verdeling

In geval van overspreiding kan ook, in plaats van een ODP, gebruik gemaakt worden van de Negatief Binomiale verdeling. Hierbij is de uitkomst Poisson verdeeld maar het gemiddelde verdeeld volgens de Gamma-verdeling. Bij de Negatief Binomiale verdeling is de spreiding verplicht één en wordt er een overspreidingsparameter (k) toegevoegd. De overspreidingsparameter zorgt ervoor dat het gemiddelde weer boven de variantie komt te liggen.

De variantie functie van de Negatief Binomiale verdeling ziet er als volgt uit: V(µ) = µ(1 + k µ).

2.1          Stap 1: Bepalen doelen en doelstellingen

Bekijk aan het begin van het project naar welke doelen bereikt moeten worden. Kijk hierbij welke tussenstappen genomen moeten worden en welke resultaten geboekt moeten worden. Op basis hiervan kan een planning gemaakt worden.

2.2          Stap 2: Communiceren met de opdrachtgevers

De belangrijkste stap is communicatie met de opdrachtgevers. Dit geldt voor de gehele looptijd van de samenwerking. Het is belangrijk altijd op te hoogte te zijn van de eisen van de opdrachtgever. Het kan namelijk voorkomen dat de uiteindelijke resultaten niet overeenkomen met de wensen van de opdrachtgever. Om dit te voorkomen is goede communicatie erg belangrijk.

2.3          Stap 3: Data verzamelen en valideren

Data verzamelen en valideren is de langstdurende stap van het gehele proces. Voor het uitvoeren van een GLM is namelijk wel data nodig. Deze data moet vervolgens nog wel gevalideerd worden. De data kan namelijk allemaal verschillende fouten bevatten, al zij het slordigheidsfouten of verkeerde metingen. Door de data te valideren filter je de foute data uit de dataset. Alleen wanneer deze stap voltooid is kan er pas begonnen worden aan de volgende stappen.

2.4          Stap 4: Data analyseren

Nadat de data verzameld en gevalideerd is, moet de data worden geanalyseerd. Dit wil zeggen dat je gaat kijken of er verbanden liggen tussen bepaalde variabelen. Op basis hiervan kan de systematische component bepaald worden en kan er zo een geloofwaardig mogelijk model worden opgezet.

2.5          Stap 5: Bepaal de modelvorm

Na het samenstellen van de systematische component is het belangrijk om de verdeling te kiezen voor het random component. Deze verdeling dient bij de doelfunctie te passen.

2.6          Stap 6: Evalueer en valideer de uitkomsten

Na het produceren van de twee componenten is het belangrijk te controleren of deze overeenkomen met de data. Vergelijk records met de gekozen grensgebieden. Wanneer dit klopt kan gezegd worden dat het GLM-model representatief is voor de realiteit.

2.7          Stap 7: Vertaal de uitkomsten naar het Nederlands

Het is belangrijk om de uiteindelijke resultaten te kunnen verklaren. Hiervoor dient ‘normaal Nederlands’ gebruikt te worden. De opdrachtgevers zijn geen wiskundigen, dus leg het zo simpel mogelijk uit.

2.8          Stap 8: Onderhouden en upgraden van het model

Na het produceren van het model is het van belang dat deze wordt onderhouden. Het model moet actueel blijven met de realiteit dus hij dient onderhouden te worden.

Het komt alleen niet vaak voor dat de policy level en de claims in dezelfde database zijn opgeslagen. De eerste stap zal dus zijn om deze twee datasets te vinden en te combineren.

Wanneer deze twee datasets lange tijd apart van elkaar zijn bijgewerkt; kunnen er problemen ontstaan bij het combineren. Hier zijn sommige vragen die hierbij kunnen ontstaan:

 Is er een verschil in moment of manier dat de twee datasets worden bijgewerkt waardoor sommige data onbruikbaar wordt?

Wanneer de databases op andere tijdseenheden worden bijgewerkt worden bepaalde records onbruikbaar omdat de bijbehorende gegevens van de andere datasets nog niet zijn bijgewerkt .

Is er een sleutel in beide databases waardoor de twee datasets gecombineerd kunnen worden op zo’n manier dat er per claim record één policy record is?

Dit moet het geval zijn wil het mogelijk zijn de twee datasets te combineren. Wanneer er meerdere policy records zijn voor één claim dan kan het combineren van de twee ervoor zorgen dat er dubbele claims worden geteld. Ook kan het zijn dat wanneer een sleutel niet elke claim paart met een policy level dat bepaalde claim records geen betekenis meer hebben.

Zijn er waarden die samengevoegd moeten worden voordat de datasets gecombineerd kunnen worden?

Denk hierbij aan de eenheid van tijd waar beide datasets aan moeten voldoen. Hierbij wordt vaak bij de policy level gekozen voor het niveau van het kalenderjaar in plaats van een kleiner niveau. Een voordeel hiervan is dat er niet rekening gehouden hoeft te worden met seizoengebondenheid, omdat het over het hele jaar is. Waar wel op gelet moet worden is policy levels die bijvoorbeeld halverwege het jaar van werking gaan. Deze zullen maar over 50% van de data effect hebben. Deze moeten dus ook alleen voor deze 50% gepaard worden.

Claim data wordt ook vaak vervoegd tot kalenderjaar. Wanneer een policy twee claims van €500 heeft in een bepaald kalenderjaar, dan zal dit in de record een claim count hebben van twee met een totale loss van €1000. Hierdoor is wel waardevolle data verloren, namelijk hoeveel loss er is bij de eerste claim en hoeveel er is bij de tweede.

Kijk bij deze stap goed naar de doelen van het model. Als er gemodelleerd moet worden over het hele bedrijf dan moet de data van alle filialen bij elkaar gecombineerd worden.

 Zijn er velden die veilig verwijderd kunnen worden?

Er kunnen velden voorkomen die in de normale wereld niet realistisch zijn. Het verwijderen van deze velden zal voordelig zijn voor het totale proces. Denk hierbij bijvoorbeeld aan aliasing (2.9). Hier moet wel goed over nagedacht worden. Het toevoegen van deze data in een later moment van het proces kan erg lastig zijn.

 Zijn er velden afwezig die wel aanwezig moeten zijn?

Er kan data zijn die niet aanwezig is die wel aanwezig moet zijn. Deze stap staat eigenlijk buiten de data preparatie, maar de uitvoerder van deze stappen moet hier toch alert op zijn. De feedback naar de opdrachtgever van dit probleem is cruciaal tot het starten van het verzamelen van nieuwe data.

Controleer op dubbele records

Wanneer twee records precies identiek zijn dan is dit waarschijnlijk het gevolg van een error. Deze controle moet gedaan worden voor de aggregatie en combinatie van de datasets.

Controleer de categoriale velden

Het kan voorkomen dat bij een categoriaal veld een andere waarde staat dan van tevoren vastgesteld is dat mogelijk is. Dit moet onderzocht worden. Het kan namelijk voorkomen dat de documentatie verouderd is.

Controleer de numerieke velden voor onrealistische waarden

Voor elk numeriek veld is een interval vastgesteld waar de waarden in moeten liggen, willen ze realistisch zijn. Wanneer de waarde hier niet in ligt zal er onderzocht moeten worden waarom dit zo is.

Beslis hoe de fouten of niet bestaande waarden behandeld moeten worden

Voor dubbele records is de behandeling simpel, verwijder één van de records.

Voor velden met onrealistische waarden is de behandeling lastiger. Wanneer al deze records verwijderd worden kan dit ervoor zorgen dat er uiteindelijk te weinig records overblijven voor het maken van een representatief model. Ook kunnen de fouten systematisch voorkomen. Dit moet eerst onderzocht worden. Een oplossing hiervoor is door de onrealistische waarden te vervangen met het gemiddelde of de modale categorie. Ook is het handig om een nieuw veld toe te voegen waarin staat dat de in de desbetreffende record een error aanwezig was.

Ook kunnen de waarden van deze onrealistische velden vervangen worden met waarden uit een nieuw model. Dit model wordt gemaakt door de records die geen errors bevatten.

Fouten in de dataset zijn niet de enige reden om de dataset aan te passen. Soms is het bijvoorbeeld voordelig om een continue variabele te converteren in een categoriale variabele (dit wordt binning genoemd). Dit kan gedaan worden om het aantal niveaus in een categoriaal veld te verlagen, om meerdere velden met elkaar te combineren tot nieuwe velden of om een enkel veld te verdelen in meerdere velden.

Gebruikelijk is om deze modificaties te maken tijdens het maken van het model.

De training set wordt gebruikt bij alle stappen van het model-bouw-proces. Denk hierbij aan het kiezen van de variabelen, de meest geschikte variabele transformaties kiezen, de verdeling kiezen et cetera.

De test set wordt gebruikt om de prestatie van het model te beoordelen en kan ook gebruikt worden om te kiezen tussen andere modellen.

Een reden waarom de data wordt gesplitst in deze twee sets is omdat wanneer de prestatie van het model getest wordt met dezelfde data waar het model gemaakt is, de beoordeling altijd een positief resultaat zal geven. Het model is namelijk gemaakt om het beste te voldoen aan de parameters van deze data.

Een andere reden is omdat er oneindig veel manieren zijn om een GLM zo complex te maken als gewenst. Er zijn veel verschillende variabelen om te includeren waarvoor elk een gewenst aantal polynomialen of hinge functions gecreëerd kunnen worden. Wanneer de complexiteit verhoogd wordt zal de training set steeds beter passen. Voor de data die niet voor het model gebruikt wordt zal de extra complexiteit de prestatie van het model niet per sé verbeteren. Het zal zelfs kunnen verslechteren.

De complexiteit van een model wordt voor een GLM gemeten in vrijheidsgraden, ofwel het geschatte aantal parameters. Per extra continue variabele zal er een vrijheidsgraad bijkomen. Voor elke extra categoriale variabele, exclusief de base-level, zal er een vrijheidsgraad bijkomen. Ook voor elk polynoom, elke hinge function, eigenlijk alles waarbij het model een nieuwe parameter moet schatten, zal ook een extra vrijheidsgraad toegevoegd worden. Elke vrijheidsgraad biedt het model meer vrijheid om beter te passen voor de training data. Meer vrijheidsgraden bieden meer flexibiliteit en daardoor zal het model altijd beter passen bij de data.

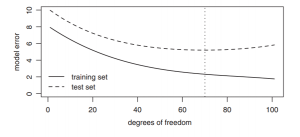
Grafiek 4.1: Effect van model complexiteit

In grafiek 4.1 is het effect te zien van wat meer complexiteit (gemeten in vrijheidsgraden) doet voor de errors (afhankelijke variabelen) van het model. Zoals te zien is zal de training set altijd beter passen dan de test set. Bij de test set is er een optimaal aantal vrijheidsgraden waarbij het model het beste zal passen.

Deze verslechtering komt door de extra flexibiliteit. Dankzij de extra flexibiliteit is het model vrij om de willekeurigheid (noise) van model te ‘verklaren’ op aanvulling tot het verklaren van het systematische effect (signal). Deze noise is uiteraard een resultaat van willekeurigheid en hoeft dus niet verklaard te worden. Een model waarin te veel noise wordt geïncludeerd wordt een overfit genoemd.

Het doel bij het modelleren is om de juiste balans te vinden waarbij er zoveel mogelijk signal wordt verklaard en zo weinig mogelijk noise. Dit is het optimum te zien in de grafiek 4.1. Om dit doel te bereiken is het dus van belang data niet mee te nemen in het model, maar om te gebruiken om het model te testen.

Aangezien de verdeelde versies van de data het hele proces gebruikt zal worden is het cruciaal dat er een goede strategie voor het verdelen geformuleerd wordt. De volgende subparagrafen beschrijft verschillende strategieën hiervoor waaronder ook een alternatief tot het verdelen van de data; genaamd kruisvalidatie.

4.3.1 Train en Test

De simpelste verdeling van de data is het creëren van twee subsets: de training set en de test set. Dit is al gedeeltelijk uitgelegd. De typische verhoudingen hiervoor zijn 60% training/ 40% test of 70% training/ 30% test. Hierbij is wel het belangrijk het volgende te overwegen: meer data beschikbaar voor de training set zorgt voor duidelijkere patronen in de data, maar als er te weinig data overblijft voor de test set dan zal de uiteindelijke beoordeling van het model minder betrouwbaar zijn.

De verdeling kan uitgevoerd worden door willekeurige records te kiezen voor beide sets of op basis van de tijdeenheid. De laatste optie heeft het voordeel dat de validatie van het model buiten de tijdperiode van de training set uitgevoerd wordt. Hierdoor geeft het resultaat een beter beeld van hoe het model zal presteren in de toekomst. Ook is dit voordeliger voor gevaren die invloed hebben op meerdere policyholders. Door het mixen van data zal er in beide sets data voorkomen waarbij een bepaald gevaar invloed heeft gehad op losses. Hierdoor zal de test set deze data niet bijzonder vinden waardoor de validatie resultaten te optimistisch zullen zijn. Door een test set te kiezen waarvan de records een andere tijdsperiode betreffen dan de training set zal de overlap geminimaliseerd worden en zal het model beter presteren over de onbekende toekomst.

4.3.2 Train, Validation en Test

Als er genoeg data beschikbaar is dan kan er ook gebruik gemaakt worden van een derde set: de validation set. Deze set wordt gebruikt om het model te verfijnen tijdens het bouwproces. De test set zal dan gebruikt worden aan het einde van het bouwproces.

Het model zal dan gemaakt worden met behulp van de training set om vervolgens beoordeeld te worden door de validation set. Op basis van deze resultaten zal het model aangepast worden. Dit is een iteratief proces.

De typische verhoudingen voor deze sets zijn 40% training/ 30% validation/ 30% test. Hierbij moet opgelet worden dat de sets niet de klein worden, anders zal hun nauwkeurigheid erg verminderen.

4.3.3 Data verstandig gebruiken

De test set moet wijs gebruikt worden. Deze dient namelijk niet te vaak gebruikt te worden. Als er te vaak gebruik gemaakt wordt van deze set of te veel keuzes van het model worden er op geëvalueerd dan zal het meer een training set worden.

Het is dus belangrijk hoe de test set gebruikt wordt. Wanneer de validation set gebruikt wordt is er meer speelruimte, maar ook deze set zal uiteindelijk verminderen in nuttigheid zodra deze te vaak gebruikt wordt. Er moet dus voor een groot gedeelte van het modelleren gebruik gemaakt worden van de ‘in-sample’ statistieken.

Het moet goed van tevoren gepland worden hoeveel en wanneer de test set gebruikt gaat worden. Kies van tevoren dus meerdere versies van het model met verschillende hoeveelheden complexiteit. Bouw en verfijn deze modellen op elk niveau van complexiteit met behulp van de in-sample statistieken (en eventueel mogelijk de validation test). Wanneer deze modellen gebouwd zijn worden ze geëvalueerd door de test set.

Wanneer een model gekozen is moet deze uiteindelijk opnieuw gebouwd worden met behulp van alle beschikbare data zodat de geschatte parameters zo geloofwaardig mogelijk worden.

4.3.4 Kruisvalidatie

Een bekend alternatief tot het splitsen van de data is kruisvalidatie. Kruisvalidatie biedt een manier om de prestatie van het model te beoordelen over onbekende data met behulp van meerdere splitsingen van train en test.

Er bestaan meerdere manieren van kruisvalidatie, maar de meest gebruikte is de k-fold kruisvalidatie. Deze werkt als volgt:

1. Splits de data in k groepen waarbij k een zelfgekozen nummer is (vaak het getal 10.) Elke groep wordt een fold. Deze splits kunnen net als bij de training/test set willekeurig uitgevoerd worden als op basis van een tijdseenheid.
2. Voor de eerste fold:
   • Train het model door de andere k-1 folds te gebruiken.
   • Test het model door de eerste fold te gebruiken.
3. Herhaal step 2 met behulp van de overgebleven folds.

Het resultaat van deze methode geeft in totaal k schattingen van de prestatie van het model. Elk van deze schattingen zijn beoordeeld met behulp van data die niet in de training set zit.

Vaak is deze manier van kruisvalidatie superieur tegenover de complete training/test splitsing; aangezien alle data gebruikt wordt voor het testen van out-of-sample­ modelprestatie in plaats van één subset. Maar deze methode heeft één groot nadeel: de ‘training’ fase van het proces moet alle bouwstappen omvatten. Bij een GLM bevat het bouwproces vooral het selecteren van variabelen en transformatie. Dit gedeelte moet ook in één keer gebouwd worden.

Wanneer alle data geëvalueerd is tijdens het beslissen welke variabelen geïncludeerd moeten worden, dan kan de overige subset niet aanschouwd worden als ‘onbekende’ data. Het kan namelijk voorkomen dat sommige variabelen alleen in het model zitten omdat deze voorkwamen in de ‘bekende’ data van de test set.

Hierdoor kan kruisvalidatie alleen gebruikt worden wanneer de selectie van de variabelen geautomatiseerd wordt. Wanneer dit het geval is kan dezelfde selectieprocedure gebruikt worden voor elke fold en komt er uit de kruisvalidatie steeds de beste schatting voor de onbekende data.

Ondanks dit worden de variabelen bij verzekeringsapplicaties vaak zelf met veel zorg en oordeel gekozen. Hierdoor is normale kruisvalidatie niet mogelijk. Daardoor is het splitsen van de data voor dit soort gevallen de voorkeur.

Kruisvalidatie kan nog steeds nuttig zijn tijdens het bouwproces. Wanneer bepaalde ‘tuning parameters’ geëvalueerd worden, bijvoorbeeld hoeveel polynomische termen gebruikt moeten worden, kan kruisvalidatie binnen de training set gebruikt worden. Hieruit kan nuttige informatie komen over hoe het model aangepast kan worden om een beter resultaat te krijgen. Echter moet het uiteindelijke model altijd geëvalueerd worden door een aparte subset die niet gebruikt is tijdens het bouwproces.

5.1.1 Frequentie/Hoogte vs. Pure Premium

Het ultieme doel van een model is om de pure premium te voorspellen, dit kan op twee manieren:

1. Bouw twee modellen, één model waar je de claim frequentie na gaat en één model waarbij je hoogte van de claims na gaat. Nadat dit is gedaan worden de modellen samengevoegd. Dit wordt gedaan door middel van de overeenkomende relatieve factoren met elkaar te vermenigvuldigen.
2. Bouw een model waarbij gericht wordt op Pure Premium. Dit kan worden gedaan door middel van de ‘Tweedie’

De tweede keuze wordt voornamelijk gebruikt als er gebrek is aan data en zo dus de twee verschillende modellen niet gemaakt kunnen worden. Het model van de claims kan dan bijvoorbeeld wel gemaakt worden maar het model voor de claim frequentie niet.

Toch wordt de frequentie/hoogte methode voorgeschreven als beste keuze.

5.1.2 Polissen met Meerdere Dekkingen en Gevaren

Het is niet altijd handig om alle gevaren in één model te stoppen. Soms is het ook verstandiger om sommige problemen apart te modelleren. Dit wordt gedaan zodat dan elk probleem apart bekeken kan worden voor elk gevaar. Een eenvoudige methode om deze aparte modellen samen te voegen is het gecombineerde alle-gevaren-model.

1. Gebruik alle aparte gevaar modellen om verwachtingen te genereren van verwachte verliezen als gevolg van elk gevaar voor een aantal blootstellingsgegevens.
2. Tel de gevaarverwachtingen bij elkaar op om voor elk record een totale kostprijs voor schade te vormen
3. Run een model op de verkregen data en gebruik de totale schadekosten die in stap 2 zijn berekend. Daarnaast zijn de zojuist gecreëerde gevaarverwachtingen de nieuwe verwachtingen voor dit model.

5.1.3 Het Transformeren van de Doelvariabele

In sommige gevallen is het handig om de doel variabele te veranderen voorafgaand aan het modelleren. Sommige overwegingen zijn:

• Voor Pure Premium, schade ratio of schademodellen. De aanwezigheid van een aantal grote verliezen kan een onnodige invloed hebben op het model. In dat soort gevallen is het slimst om de grote verliezen af te dekken. Hier komt een stabiel model uit.
• Het is ook belangrijk om te kijken naar catastrofale evenementen die voor gigantische verliezen kunnen zorgen. Als dit is gebeurd of mogelijk is moeten deze verliezen uit de dataset worden gehaald. Hiermee wordt het model gelimiteerd tot een non-catastrofaal model.
• Wanneer de gegevens risico’s bevatten die niet volledig verloren zijn, zodat er verdere schadeontwikkelingen te verwachten zijn, kan het nodig zijn om verliezen voorafgaand aan het modelleren te ontwikkelen. Deze schadeontwikkelingen moeten wel getransformeerd worden naar het type entiteit worden gemodelleerd.
• Wanneer de premie wordt gebruikt als noemer van een ratiodoelvariabele is het misschien nodig om de premie op niveau te brengen.
• Wanneer er data van meerdere jaren wordt gebruikt moeten verliezen en/of toenames in trend gezet worden.

Als er nieuwe data binnen komt is het belangrijk om te kijken of de doel variabele nog meer geperfectioneerd kan worden door de variabele toe te voegen die door middel van de data verkregen is. Voor de gebruiker is het altijd nog wel belangrijk te kijken welke variabele toegevoegd moeten worden en welke daadwerkelijk invloed hebben op het model.

Een belangrijk criterium voor een variabele is dat er een relatie tussen de voorspeller en het doel is wat geen noise is. Deze correlatie wordt bepaald door een p-waarde die wordt beschreven in paragraaf 2.3.2. De p-factor moeten worden gezien als een stuk informatie waarvan goed geïnterpreteerd moet worden of de variabele invloed heeft op de doelvariabele.

Naast statistische significantie zijn er ook andere overwegingen voor variabele selectie zoals:

• Zal het effectief zijn voor de kosten om de waarde van deze variabele over te nemen wanneer er wordt gewerkt aan een nieuwe zaken?
• Voldoet de opname van de variabele in een rating plan aan actuariële standaarden van praktijk- en regelgevingsvereisten?
• Kan het elektronische offerte systeem eenvoudig worden aangepast om de opname van deze variabele in het ratingplan?

Wanneer een continue variabele (gelogd) wordt toegevoegd aan een log-link model gaat het model er van uit dat er een lineaire relatie is tussen de log van de variabele en de log link. Sommige variabelen hebben alleen een complexere relatie met de target variabele die niet lineair is. Wanneer dit het geval is moeten er transformaties uitgevoerd worden met de variabele zodanig dat deze zijn effect goed kan modelleren.

5.4.1 Niet-Lineaire Trends Herkennen met Partial Residual Plots

De set van partial residuals voor elke predictor x_j in een model wordt als volgt weergegeven:

r_i = (y_i – µ_i) * g’(µ_i) + β_jx_ij

Hierbij is g’(µ_i) de eerste afgeleide van de link functie. Bij het geval van een log-link­ model zal de verhouding als volgt versimpelt kunnen worden:

r_i = ((y_i – µ_i)/ µ_i) + β_jx_ij

In de laatste verhouding wordt de residual uitgerekend door de verwachting van het model af te trekken van de daadwerkelijke waarde, om vervolgens op dezelfde schaal gebracht te worden als de lineair predictor door gedeeld te worden door µ_i. Vervolgens wordt het gedeelte van de linear predictor waar x_j verantwoordelijk voor is (β_jx_ij) terug toegevoegd aan het resultaat.

De partial residual kan dus ook gezien worden als de daadwerkelijke waarde met alle componenten van de voorspelling (behalve dan het gedeelte gedreven door de aftrekking van x_j). De variantie in de partial residuals bevat dus de onverklaarde variantie naast het gedeelte van de variantie die het model wel probeert te verklaren met behulp van de β_jx_ij. Deze residuals kunnen vervolgens geplot worden tegenover de schattingen uit het model om ze zo te kunnen beoordelen.

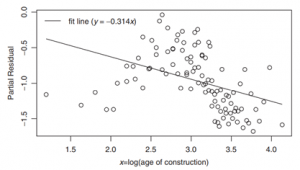
Grafiek 5.1: Partial Residuals geplot                                          

In grafiek 5.1 is zo’n plot te zien. De lineaire verwachting is in de grafiek geplot samen met de partial residuals van de variabele. Ondanks deze lijn misschien de beste lineaire lijn is voor deze data, is deze lijn nog steeds niet het beste model. Het is duidelijk dat er iets flexibeler nodig is dan een rechte lijn. Hier worden in de komende subparagrafen drie manieren uitgelegd om zulke niet-lineaire modellen op te stellen in een GLM:

• de variabele ‘binnen’.
• polynomiale termen toevoegen.
• stuksgewijze lineaire functies gebruiken.

5.4.2 De Variabelen Binnen

Een manier is om niet te modelleren met een continue variabele maar om te modelleren met een categoriale variabele. De continue variabele wordt hierbij gebinned: een nieuwe categoriale variabele wordt gecreëerd waarbij de niveaus gelijk staan aan de intervallen over het bereik van de originele variabele. Vervolgens zal het model deze variabele als elk andere categoriale variabele behandelen. Voor elk interval zal een coëfficiënt geschat worden die voor elk risico geldt die hier binnen valt.

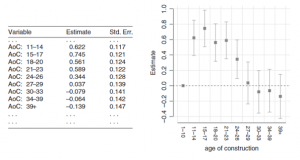
Grafiek 5.2: de geschatte coëfficiënten voor de ‘gebinde’ variabele met rechts een grafische representatie

Grafiek 5.2 laat de variabele zien als categoriale variabele. In dit voorbeeld zijn tien ‘bins’ gecreëerd. De grenzen zijn zo gekozen dat elke bin ongeveer dezelfde aantal records bevat en als base-level is de building-age van 1 tot 10 gekozen.

Zoals te zien is in de grafiek nemen de boxplots van de coëfficiënten dezelfde vorm aan als de grafiek van de partial residuals. Een continue variabele binnen zorgt ervoor dat het model vrij komt van de aangenomen relatie met de target variabele van lineair tot elke soort vorm.

Ondanks dit zijn er toch nadelen aan deze aanpak. Het binnen van een continue variabele zorgt voor een groot aantal parameters in het model waardoor het model niet meer simpel is. Het is niet wijs om meer vrijheidsgraden toe te voegen dan nodig is om een model goed over de data te laten passen.

Ook wordt de continuïteit van de schattingen niet gegarandeerd. Het toelaten tot vrije beweging van de intervallen is niet per sé een goed iets. Elke schatting is onafhankelijk van elkaar gemaakt en er is geen reden om ervan uit te gaan dat dit continu werkt. Hierdoor is er een risico dat sommige schattingen niet overeen komen met andere schattingen vanwege de toevoeging van te veel noise.

In grafiek 5.2 is dit te zien bij de bin: 21-23 jaar. Het ziet er namelijk uit dat hij zal blijven dalen na 17 jaar. Ondanks dit is de factor van de bin van 21-23 jaar net wat hoger dan die van de 18-20 jaar. Er is geen reden om te geloven dat dit patroon realistisch is. Het is hoogst waarschijnlijk het resultaat van de beweeglijkheid van de data.

De variatie binnen de intervallen wordt tevens ook genegeerd. Aangezien elke bin elk een enkele schatting toegewezen krijgen, zal het model de variatie in hoogte negeren. Natuurlijk kan dit tegengegaan worden door de grenzen van de intervallen te verfijnen door de bins verder te splitsen. Het nadeel hiervan is wel dat de data verder uitgedund wordt en dus gevoeliger wordt tot noise.

5.4.3 Polynomiale Termen Toevoegen

Een andere manier om niet-lineaire trends in een lineair model te laten werken is door het toe te voegen van polynomiale termen naast de originele variabele. Deze termen en variabele zullen elk als eigen predictor aanschouwd worden en er zal dus voor elk een eigen coëfficiënt geschat worden. Hierdoor zullen krommen in de data gemodelleerd kunnen worden; des te meer polynomiale termen, des te flexibeler het model wordt.

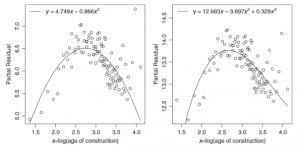
Grafiek 5.3: De partial residuals plot met twee polynomiale termen (links) en drie polynomiale termen (rechts)

De linker grafiek in grafiek 5.3 laat het resultaat zien van het toevoegen van het kwadraat van de variabele tot het model. Dit is duidelijk al een beter model voor de data dan de lineaire lijn.

De rechter grafiek in grafiek 5.3 laat het resultaat zien van het toevoegen van zowel het kwadraat, als de drie-macht van de variabele tot het model. Dit is misschien een nog beter model dan de linker aangezien de stijging van de data aan het eind verklaard wordt.

Eén groot potentieel nadeel tot het gebruiken van polynomiale termen is het verlies van interpreteerbaarheid. Met alleen de coëfficiënten is het erg lastig om achter de vorm van de kromme te komen. Om de relatie tussen de predictor en de target variabele goed te begrijpen is het misschien nodig om de polynomiale functie te plotten.

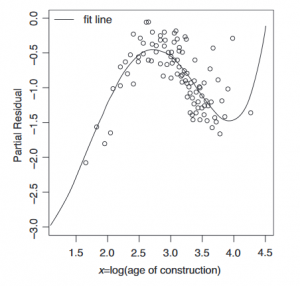
Grafiek 5.4: Partial Residuals plot met vijf polynomiale termen

Een ander nadeel is dat polynomiale functies vaak aan het einde van de data zich raar gaat gedragen. Dit is te zien in grafiek 5.4.

5.4.4 Stuksgewijze Lineaire Functies Gebruiken

Een derde methode om niet-lineaire trends te modelleren is door de lijn te ‘breken’ en stuksgewijs lineair te werk te gaan. Hierdoor kan de helling aangepast worden per ‘break point’.

Deze ‘break point’ zal zijn op het punt dat de lineaire lijn de data niet meer goed genoeg representeert. Dit wordt gedaan door een nieuwe variabele toe te voegen: max(0,ln(AoC)-2,75). Hierbij is de ‘2,75’ het punt waar de lijn de data niet goed meer representeert. Deze nieuwe variabele wordt de hinge function genoemd. Per hinge function komt er een nieuw vrijheidsgraad bij. Deze hinge function zal voor alle waardes lager dan de log waarde van 2,75 een nul teruggeven. Hierna zal hij lineair anders werken.

De coëfficiënt die bij de hinge function zal horen geeft aan op wat voor manier de helling zal veranderen. Als de helling eerst 2 is, en de coëfficiënt van de hinge function -3 is, dan betekend dit dat de helling op het punt dat de hinge function ten werk gaat gelijk zal zijn aan (2 + -3 =) -1. Dit is te zien in grafiek 5.5.

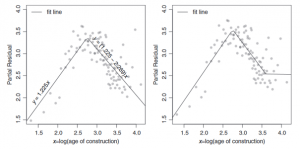
Grafiek 5.5: Partial Residual plot met één breaking point op 2,75 (links) en twee breaking points, op 2,75 en op 3,6 (rechts)

Het gebruik van hinge functions biedt de gebruiker de mogelijkheid een model te produceren die niet-lineaire patronen kan plotten. Ondanks dit zijn er toch nadelen aan deze methode:

De breaking points zullen handmatig gekozen moeten worden door de gebruiker. Deze breaking points zijn in principe een gok gekozen door de inspectie van de data. Een GLM biedt geen geautomatiseerde versie van het kiezen van de breaking points.

Ook is een nadeel dat, ondanks dat de kromme nog wel continu is, de eerste afgeleide niet meer continu zal zijn. De passende lijn zal dus niet de ‘vloeiende’ kwaliteit bevatten die wordt verwacht.

5.4.5 Natural Cubic Splines

Een meer geavanceerdere methode tot het handelen van niet-lineaire patronen is het gebruikmaken van natural cubic splines. Hierbij worden de concepten van polynomiale functies en stuksgewijze functies met breaking points gecombineerd. Deze methode is wiskundig complexer dan de andere twee. Hier wordt verder niet op ingegaan, maar hier zijn een paar van de karakteristieken:

• De eerste en tweede afgeleide zijn continu. De kromme zal dus compleet vloeiend lijken.
• De fits aan de randen van de data worden beperkt tot een lineaire functie. Hierdoor kunnen de rare wendingen van de polynomiale functies niet meer optreden.
• Dankzij het gebruik van de hinge functions zal het model beter bij de data passen dan normale polynomiale functies.

Deze samenhang is mogelijk met verschillende soorten variabelen. Zo kunnen twee categoriale variabele tot een interactie lijden. Ook kunnen twee continue variabele lijden tot een interactie. Het kan ook het geval zijn dat één continue variabele en één categoriale variabele lijden tot een interactie.

5.6.1 Interactie tussen twee Categoriale Variabelen

Voorbeeld

Er is een claimfrequentie model welke Poisson verdeeld is en het model gebruikt een log link. Er worden twee categoriale variabelen gekozen: bezettingsklassen (genoteerd als 1 t/m 4), waarbij klasse 1 de basis klasse is en we nemen de categoriale variabele: sprinkler status. Hierbij zullen de variabelen ja/nee bevatten (als in wel of geen sprinkler systeem).

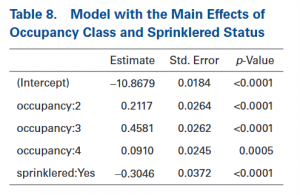
De resultaten na het uitvoeren van het model zijn weergegeven in tabel 8. De coëfficiënt -0,3046 impliceert ‘sprinklered:yes’ waarvan weer geïmpliceerd wordt dat er een korting is van 26,3 (e^-0,3046) -1 <= log link.

Er wordt nu getest of de ‘sprinklered korting’ varieert binnen de verschillende bezettingsklassen. Om dit te doen wordt de interactie van deze twee variabelen toegevoegd aan het model. Achter de schermen voegt het modelsoftware twee kolommen toe. Beide kolommen staan voor niet basisniveaus van de twee variabelen. Wanneer een risico een bepaalde combinatie bevat zal in deze kolommen de waarde ‘1’ staan. Als dit niet het geval is komt de waarde ‘0’ hierin te staan. Deze nieuwe kolommen worden beschouwd als afzonderlijke voorspellers. Deze nieuwe voorspellers geven het risico aan wanneer deze combinaties voorkomen. In dit voorbeeld resulteert dat in drie nieuwe toegevoegde voorspellers: de combinatie van ‘sprinklered yes’ bij bezetting 2, 3 en 4.

De uitvoeringen zijn in tabel 9 weergeven.

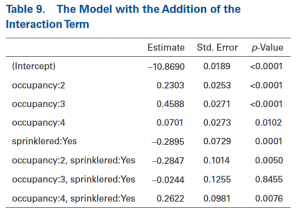
Bij de eerste rij van de interactietermen is een negatieve coëfficiënt gegeven van -0,2847. Dit geeft dus aan dat bezettingsklasse 2 een steilere korting zal hebben dan bezettingsklasse 2. Als deze waarde ingevuld wordt in de functie komt het antwoord namelijk op:

e^(-0,2895-0,24847) -1 = 43,7 korting

De lage p-waarde laat zien dat er een significant verschil is tussen bezettingsklasse 1 en 2.

De interactie met bezettingsklasse 3 laat ook een negatieve coëfficiënt zien. De p-waarde voor deze interactie is alleen zeer groot. Er is dus geen significant verschil. Op basis hiervan kan het model vereenvoudigd worden door middel van het combineren van klasse 3 en de basis klasse.

De interactiewaarde met bezettingsklasse 3 heeft een significante positieve waarde. Dit wil zeggen dat klasse 4 misschien helemaal geen korting hoeft te krijgen.

5.6.2 interactie met een categoriale variabele en een continue variabele

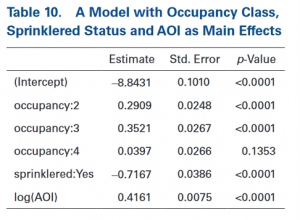
Verdergaand met het bovenstaande voorbeeld wordt er een continue variabele (AOI) aan het model toegevoegd. Het model met de belangrijkste effecten levert de uitkomsten op die zijn te zien in tabel 10. Door middel van de zogenaamde AOI-curve kan bepaald worden of het anders is als er wel sprinklers aanwezig zijn. Om dit te bepalen moet de interactie tussen deze twee variabelen toevoegt worden. De GLM-software voegt nu een rij toe in de matrix. De uitkomsten van dit model zijn te zien in tabel 11.

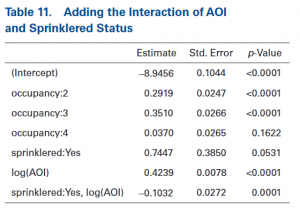
In tabel 11 is te zien dat er een waarde van interactie is die gelijk is aan -0,1032. Dit wil zeggen dat de toename van de frequentie wat in reactie staat met AOI minder scherp is met gebouwen waar een sprinkler-systeem aanwezig is. De p-waarde toont aan dat er een significant verschil is.

De linker grafiek in grafiek 5.5 laat de grafische vorm van dit model zien. Hierin is de invloed te zien van de AOI en de sprinklered status. Te zien is dat de lijn voor wel-sprinklered minder stijl is dan de niet-sprinklered lijn.

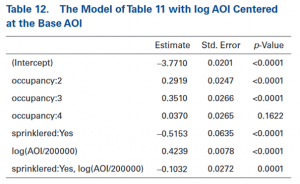
Het model kan ook op een andere manier bekeken worden: door het delen van AOI door de basis AOI. Dit is gedaan en dat gaf de volgende uitkomsten die in tabel 12 te zien zijn.

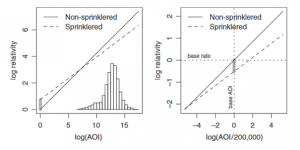
Grafiek 5.5: Illustration of the Effect of the Interaction of Sprinklered and Amount of Insurance (left panel) and the Same Model After Dividing AOI by Its Base Amount (right panel)

Dit model is identiek aan het andere model alleen zijn de verhoudingen anders. De negatief sprinklered waarde refereert nog steeds naar de waarde waar AOI 0 is. De rechter afbeelding in grafiek 5.5 is de illustratie van dit model.

5.6.3 interactie met 2 continue variabelen

Om de laatste mogelijke interactie te begrijpen is het handig om het effect te visualiseren. In figuur 15 is dit verschil goed te zien. In de rechter afbeelding is een scenario te zien waar twee variabelen in een model zitten met gemiddelde effecten alleen.

Wanneer deze variabelen samen een interactie vormen wordt de rechter afbeelding gevormd. Het stijgt harder dan de normale vorm. Zo is makkelijk het verschil te zien van als de variabelen zijn samengevoegd en wanneer niet.